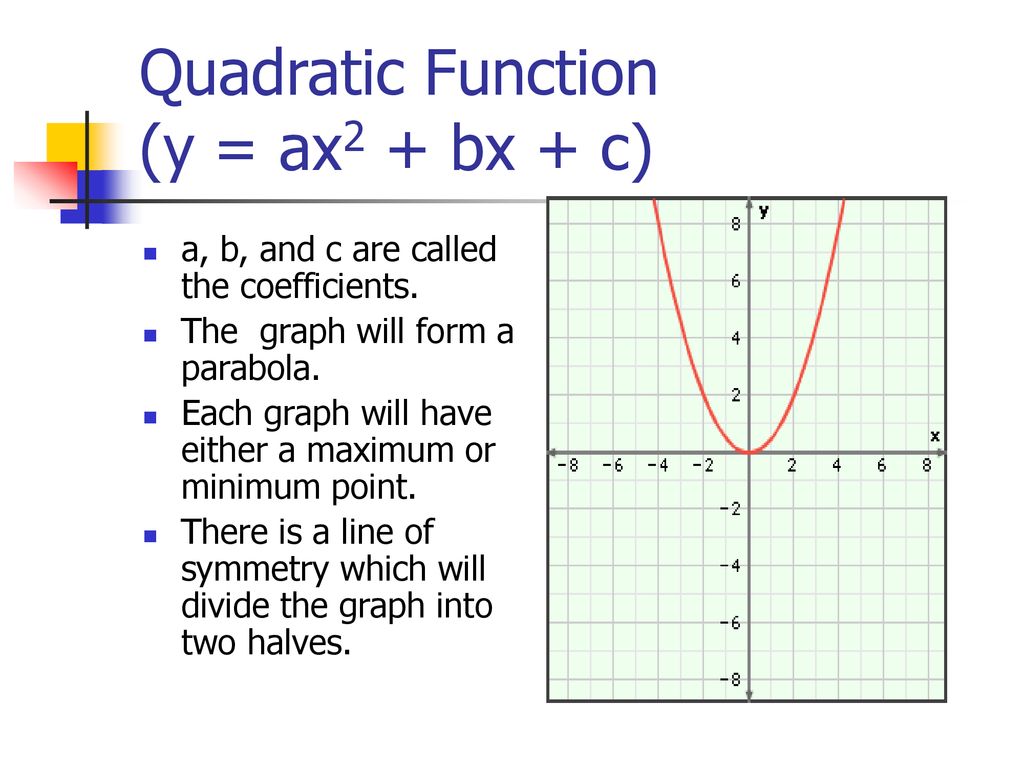
In the next few questions, we will find the roots of the general equation y = a x 2 b x with a ≠ 0 by factoring, and use that to get a formula for the axis of symmetry of any equation in that form Question 5 We want to factor a x 2 b x Because both terms contain an x, We learned from the video lesson that the b value in the quadratic equation y = ax2 bx c affects the location of the parabola Each parabola has the same a value Each parabola has the same a valueThe graph of y = ax^2 bx c is called a quadratic function
How Do You Graph F X 3x 2 4x 1 Socratic
Y=ax2+bx+c how to find b
Y=ax2+bx+c how to find b-Exploring Parabolas by Kristina Dunbar, UGA Explorations of the graph y = ax 2 bx c In this exercise, we will be exploring parabolic graphs of the form y = ax 2 bx c, where a, b, and c are rational numbers In particular, we will examine what happens to the graph as we fix 2 of the values for a, b, or c, and vary the third We have split it up into three partsRewrite the equation as ax2 bx c = y a x 2 b x c = y Move y y to the left side of the equation by subtracting it from both sides Use the quadratic formula to find the solutions Substitute the values a = a a = a, b = b b = b, and c = c−y c = c y into the quadratic formula and solve for x x Simplify the numerator



Suppose A Parabola Y Ax 2 Bx C Has Two X Intercepts One Pos
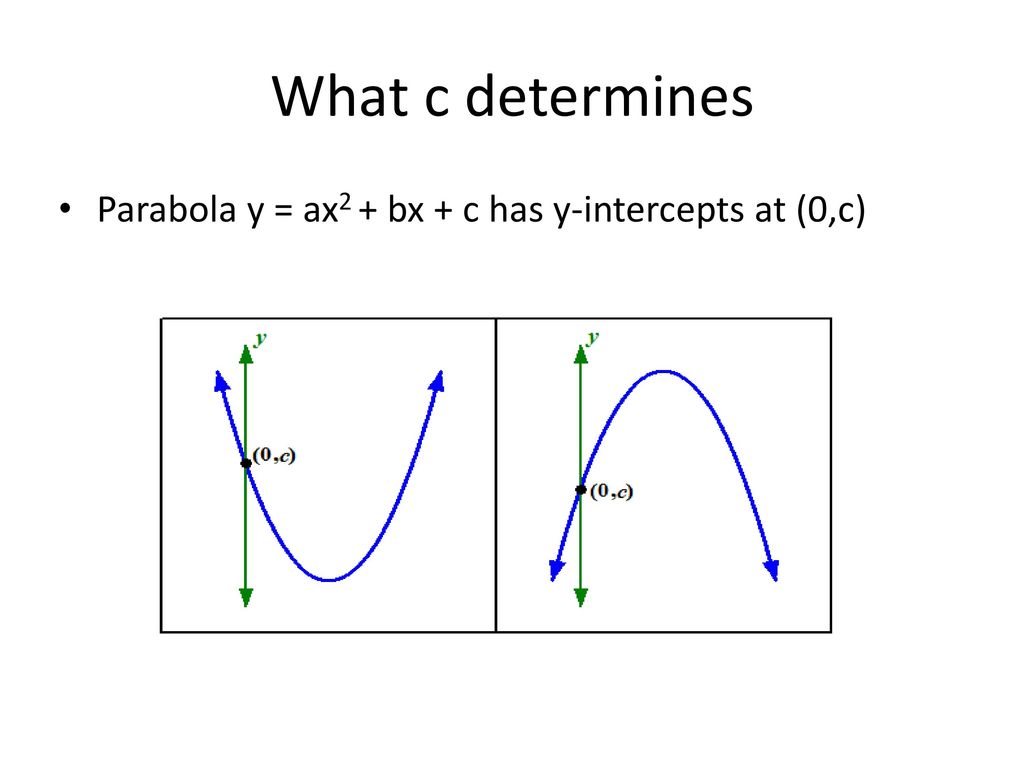
Question A Quadratic Function Is A Function Of The Form Y=ax2bxc Where A, B, And C Are Constants Given Any 3 Points In The Plane, There Is Exactly One Quadratic Function Whose Graph Contains These Points Find The Quadratic Function Whose Graph Contains The Points (0, 3), (1, −6), And (4, −81)Categories English Leave a Reply Cancel reply Your email address will not be published Required fields are marked * Roles of a, b, c 3 The Standard Formula for Quadratic Functions b helps determine the axis of symmetry (and turning point) for a parabola ax2 bx c = 0 The Standard Formula for Quadratic Functions c represents a vertical change of the graph (yintercept) ax 2 bx c = 0
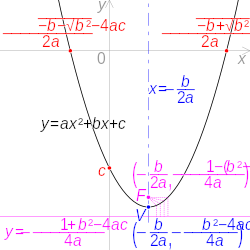
Mathematics Middle School answer answered The graph of y = ax 2 bx c is a parabola that opens up and has a vertex at (2, 5) The focus turns out to be at $(\frac{b}{2a},\frac{1b^2}{4a}c)$ Notice how the vertex and focus are lying on the same line That's to be expected with the equation for "vertical" parabolas that you described Solution Get the equation in the form y = ax2 bx c Calculate b / 2a This is the xcoordinate of the vertex To find the ycoordinate of the vertex, simply plug the value of b / 2a into the equation for x and solve for y This is the ycoordinate of the vertex
Of that vague equation, the X coordinate is at b/2a To find the Y coordinate, plug it back in Now if you would like to do this the calculus way, differentiate the equation, and set the resulting 2ax = b and solve for X Then, plug the X backThis is your generic quadratic equation y = ax 2 bx c Move the loose number over to the other side y – c = ax 2 bx Factor out whatever is multiplied on the squared term Make room on the lefthand side, and put a copy of " a " in front of this spaceAnswer y = ax2 bxc The vertex will correspond to the point where the curve attains a minima (a> 0) or maxima (a < 0) ∴ dxdy = 2axb = 0 ⇒ x = 2a−b




Suppose A Parabola Y Ax 2 Bx C Has Two X Intercepts One Pos



Quadratic Function Wikipedia
The square root of the same, less the coefficient of the middle term, beingYour equation will have the formula y = Ax^2 Bx C (writing it as Ax^2 Bx C = y may help your math) Your three (x, y) points can be plugged into this formula to to get a system of three equations in A, B, and C, which can be solved by substitution or elimination to obtain A, B, and CThe formula for the x position of the vertex is Now using the points, Now substitute for b




Quadratic Graph Example Y Ax Expii



Quadratic Function By Mr Keung Ms Keung Ppt Download
Since y = mx b is an equation of degree one, the quadratic function, y = ax2 bx c represents the next level of algebraic complexity The parabola also appears in physics as the path described by a ball thrown at an angle to the horizontal (ignoring air resistance)If y=ax^(2)bxc is the reflection of parabola y=x^(2)4x1 about the line y=3,abc= The locus of the middle points of all chords of the parabola y^(2)=4ax passing through the vertex is y=a(x2)(x4) In the quadratic equation above, a is a nonzero constantFactoring ax2 bx c This section explains how to factor expressions of the form ax2 bx c, where a, b, and c are integers First, factor out all constants which evenly divide all three terms If a is negative, factor out 1 This will leave an expression of the form d (ax2 bx c), where a, b, c, and d are integers, and a > 0




3 The Curve Y Ax2 Bx C Where A B And C Are C Gauthmath




Graph Of Y Ax 2 Bx C Novocom Top
Any equation which is formed like ax² bx c = 0 is a Quadratic Equation, where a is a quadratic coefficient, b is a linear coefficient and c is a constant In the equation, "a" is a nonzero value The equation becomes linear if "a" in the equation equals to zero The highest exponent of the equation is always 2 By solving the equationLuxmed lublin112 lublin lucyfer luca lukas podolski luka rosi luzowanie obostrzeń lubimy czytać lucyfer sezon 6 y=ax^2bxc (a b) (b c) (c a) y=ax2bxc find a b c y=ax^2bxc find a b c y=ax2bxc what is a b and c y=ax^2bxc what is a b and c y=ax2bxc what is a b and c y=ax^2bxc what is a b and cGiven curve y = a x 2 b x c y = a x ^ { 2 } b x c y = a x 2 b x c It is given that the curve passes through the point ( 1, 2) (1,2) ( 1, 2) Thus a ( 1) 2 b ( 1) c = 2 ⇒ a b c = 2 \begin {gather} a\left ( 1\right) ^ {2}b\left ( 1\right) c = 2 \\ \Rightarrow abc=2 \end {gather} a ( 1) 2 b ( 1) c = 2 ⇒ a b c = 2
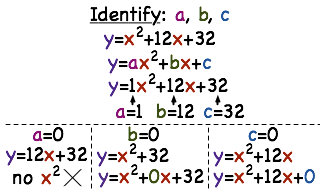



How Do You Find The A B And C Values Of A Quadratic Function Printable Summary Virtual Nerd




Find The Sign Of A B C In Ax 2 Bx C Given The Graph And A Coordinate On It Mathematics Stack Exchange
The red graph is y = ax2 bx c y = ax 2, the basic parabola will always be in red in future examples for comparison purposes Notice that when the value for variable 'a' is positive, the minimum of the graph does not change even though the value for variable 'a' was changed(The vertex formula is derived from the completingthesquare process, just as is the Quadratic FormulaSolution The equation of the trajectory of a projectile motion is y = x t a n θ − g x 2 2 u 2 c o s 2 θ y = x t a n θ ( 1 − g x u 2 2 t a n θ c o s 2 θ) = x t a n θ ( 1 − g x u 2 s i n 2 θ) = x t a n θ ( 1 − x R) ( i) where R is the horizontal range of the projectile From the given equation of projectile y = a x − b x
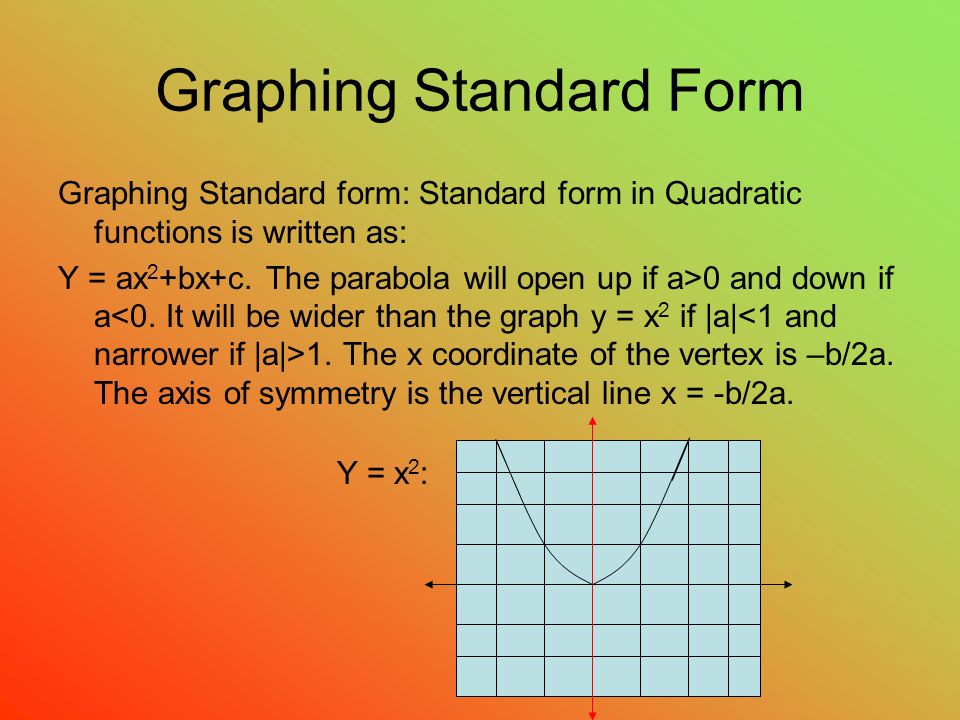



Quadratic Formula Sam Scholten Graphing Standard Form Graphing Standard Form Standard Form In Quadratic Functions Is Written As Y Ax 2 Bx C The Ppt Download




B Value Definition Explanation Video Lesson Transcript Study Com
y = ax2 bx c ← c is a constant ⇒ dy dx = 2ax2−1 bx1−1 0 = 2ax1 bx0 0 = 2ax bThe equation `y=ax^2bxc` is a means of describing the quadratic function If a quadratic function is equal to zero, the result will be a quadratic equation with The axis of symmetry always passes through the vertex of the parabola The x coordinate of the vertex is the equation of the axis of symmetry of the parabola For a quadratic function in standard form, y=ax2bxc , the axis of symmetry is a vertical line x=−b2a



Unique Quadratic Equation In The Form Y Ax 2 Bx C



Quadratic Function Y Ax 2 Bx C Quadratic
Question 2519 A parabola y = ax^2 bx c has vertex (4, 2) If (2, 0) is on the parabola, then find the value of abc Answer by Fombitz() (Show Source) You can put this solution on YOUR website! Y = ax 2 bx c Move the loose number over to the other side y – c = ax 2 bx Factor out whatever is multiplied on the squared term Make room on the lefthand side, and put a copy of "a" in front of this spaceI'm dealing with quadratic equations (y=ax2bxc) and I need to know what the three variables, a, b and c stand for I'm pretty sure c is the yintercept, and I think b is used toThe standard form is ax² bx c = 0 with a, b, and c being constants, or numerical coefficients, and x is an unknown variable Considering this, what form is y ax2 bx c?



If Y 2 Ax 2 Bx C Then Y 3 D 2y Dx 2 Is A A Constant Sarthaks Econnect Largest Online Education Community



How To Draw A Parabola Ppt Download
Steps for Solving Linear Equation a x b x = c − a x b x = c Subtract \left (a\right)x from both sides Subtract ( − a) x from both sides bx=c\left (a\right)x b x = c − ( − a) x Multiply 1 and 1 to get 1 Multiply − 1 and − 1 to get 1Here are the three forms a quadratic equation should be written in 1) Standard form y = ax2 bx c where the a,b, and c are just numbers 2) Factored form y = (ax c) (bx d) again the a,b,c, and d are just numbers 3) Vertex form y = a (x b)2 c again the a, b, and c are In the same manner what are the forms of quadratic equations?



The Graph Of Y Ax 2 Bx C Has A Minimum At 5 3 And Passes Through 4 0 How Do I Find The Values Of A B And C Quora




How Do You Graph F X 3x 2 4x 1 Socratic
How to Find the Axis ofSymmetry y = ax2 bx c The line for the axis of symmetry crosses over the number achieved by doing the formula –b/2a 9 Problem 1 Formula y = ax2 bx c y = 5x2 10x – 3 Directions find the vertex, yintercept and axis of0$ Find the sign of the coefficient $c$ I'm having difficulties with this problem What I've0 Answers 0 votes answered by Citrix Best answer Answer C




Clockwise Markers For The Functions Linear Y Ax B Quadratic Y Download Scientific Diagram




Perhatikan Grafik Berikut Jika Persamaan Grafik Tersebut Adalah Y Ax 2 Bx C Maka Nilai Dari Brainly Co Id
The square trinomial $y=ax^2 bx c$ has no roots and $a b c >The graph of the quadratic y = ax^2 bx c has the following properties (1) The maximum value of y = ax^2 bx c is 5, which occurs at x = 3 (2) The graph passes through the point (0,13) If the graph passes through the point (4,m), thenY = ax 2 bx c A suitable conclusion statement from such a relationship would be that y is quadratic with x y varies quadratically with x y is a quadraticCalculator Use This online calculator is a quadratic equation solver that will solve a secondorder polynomial equation such as ax 2 bx c = 0 for x, where a ≠ 0, using the quadratic formula The calculator solution will show work using the quadratic formula to solve the entered equation for real and complex roots




Graphing Y Ax2 Bx C Youtube



Show That Y Ax 2 Bx C A 0 Represents A Parabola And Find Its Vertex Focus Directrix And Latus Rectum Sarthaks Econnect Largest Online Education Community
If y = ax^2 bx c passes through the points (3,10), (0,1) and (2,15), what is the value If y = ax^2 bx c passes through the points (3,10), (0,1) and (2,15), what is the value of a b c?In 628 AD, Brahmagupta, an Indian mathematician, gave the first explicit (although still not completely general) solution of the quadratic equation ax 2 bx = c as follows "To the absolute number multiplied by four times the coefficient of the square, add the square of the coefficient of the middle term; Standard form of a quadratic equation is y=ax2bxc, where 'a' is not 0 Vertex form of a quadratic equation is y=a(xh)2k, where (h,k) is the vertex of the quadratic function How do you find H and K?




Graph Of Y Ax 2 Bx C Novocom Top




Aim Review Of Parabolas Graphing Do Now Write Down The Standard Equation Of A Parabola Answer Y Ax 2 Bx C Homework Workbook Pg 427 Part Ppt Download
The quadratic equation itself is (standard form) ax^2 bx c = 0 where a is the coefficient of the x^2 term b is the coefficient of the x term c is the constant term you use the a,b,c terms in the quadratic formula to find the roots the minimum / maximum point ofSuppose you have ax 2 bx c = y, and you are told to plug zero in for y The corresponding xvalues are the xintercepts of the graph So solving ax 2 bx c = 0 for x means, among other things, that you are trying to find xintercepts Since there were two solutions for x 2 3x – 4 = 0, there must then be two xintercepts on the graph Graphing, we get the curve below A quadratic function is a function of the form y = ax2 bx c, where a≠ 0, and a, b, and c are real numbers How does b affect the parabola?




1 Which Of The Following Models Best Describes The Chegg Com
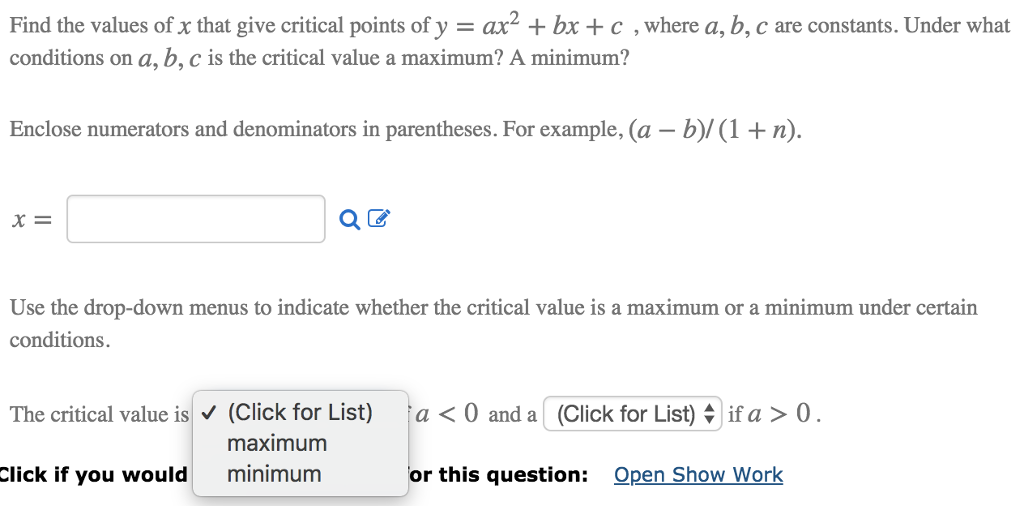



Find The Values Of X That Give Critical Points Of Y Chegg Com
When we find the maximum value and the minimum value of ax 2 bx c then let us assume y = ax 2 bx c Or, ax 2 bx c – y = 0 Suppose x is real then the discriminate of equation ax 2 bx c – y = 0 is ≥ 0 ie, b 2 – 4a(c – y) ≥ 0 Or, b 2 – 4ac 4ay ≥ 0Find the derivative of y = ax^2 bx C Assume that a, b and c are constants dy/dx = Question Find the derivative of y = ax^2 bx C Assume that a, b and c are constants dy/dx = This problem has been solved!When b = 0, the vertex of the parabola lies on the yaxis Changing b does not affect the shape of the parabola (as changing a did)
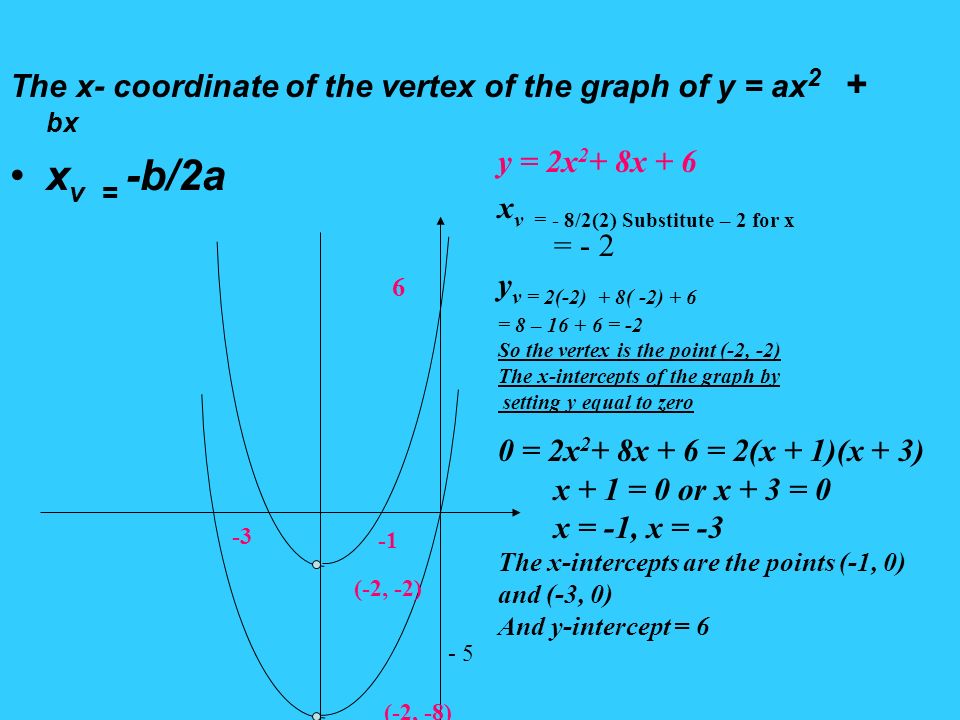



Chapter 4 Applications Of Quadratic Models To Graph The Quadratic Equation Y Ax 2 Bx C Use Vertex Formula X V B 2a Find The Y Coordinate Ppt Download
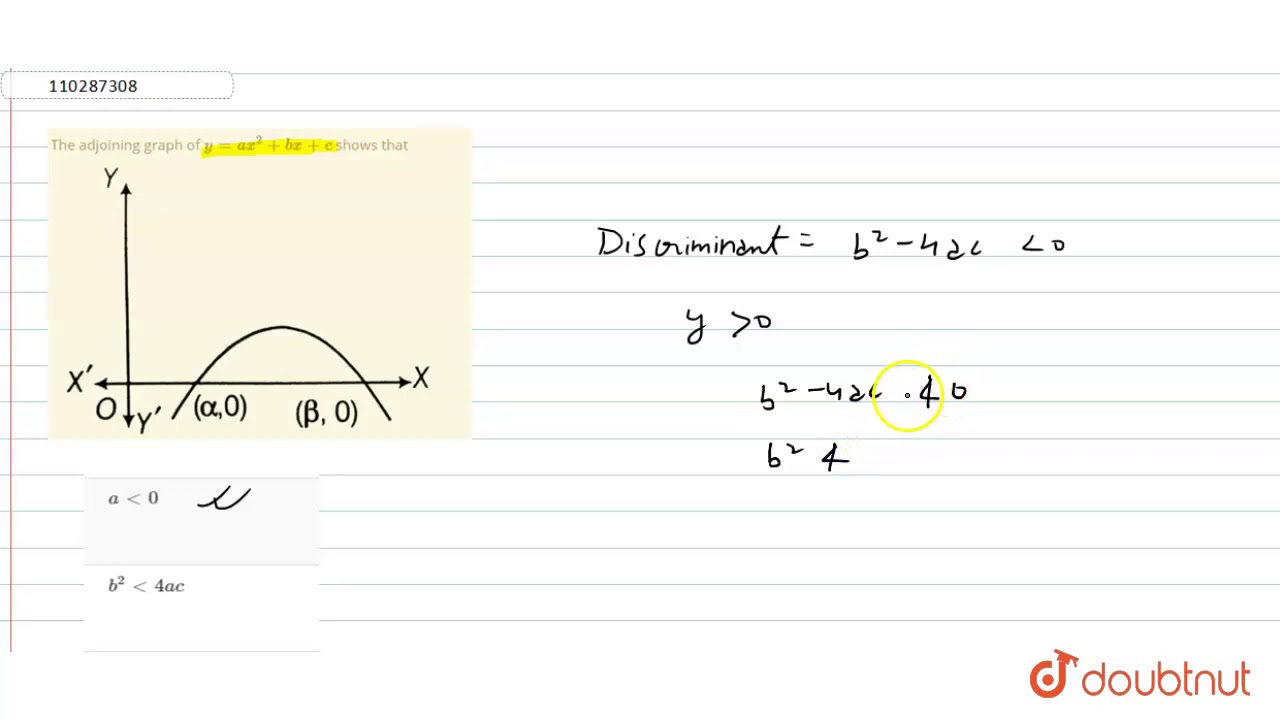



The Adjoining Graph Of Y Ax 2 Bx C Shows That Youtube
Find in the form y= ax^2 bx c, the equation of the quadratic whose graph a) touches the xaxis at 4 and passes through (2,12) b) has vertex (4,1) and passes through (1,11) Answer provided by our tutors y= ax^2 bx c a) touches the xaxis at 4 and passes through (2,12)The graph of y = ax2 bx c is given in the figure Solve the equation asked in Mathematics by styla A x = 2 B x = 2 C No real solutions D x = 0 algebraandtrigonometry;For example, a univariate quadratic function has the form f = a x 2 b x c, a ≠ 0 {\displaystyle f=ax^{2}bxc,\quad a\neq 0} in the single variable x The graph of a univariate quadratic function is a parabola whose axis of symmetry is parallel to the yaxis, as shown at right If the quadratic function is set equal to zero, then the result is a quadratic equation The solutions to the



How To Determine A Quadratic Function Y Ax 2 Bx C If Its Graph Passes Through The Point 2 19 And It Has A Horizontal Tangent At 1 8 Quora




Consider The Graph Of F X Ax 2 Bx C In The Adjacent Figure We Can Conclude That
See the answer See the answer See theGiven y = ax 2 bx c , we have to go through the following steps to find the points and shape of any parabola Label a, b, and c Decide the direction of the paraola If a > 0 (positive) then the parabola opens upward If a < 0 (negative) then the parabola opens downwardIn the quadratic equation a x 2 b x c = 0, a = 0, Δ = b 2 − 4 a c a n d α β, α 2 β 2, α 3 β 3 are in GP where α, β are the root of a x 2 b x c = 0 then View solution What is the sum of the roots of the quadratic equation x 2 x 1 = 0
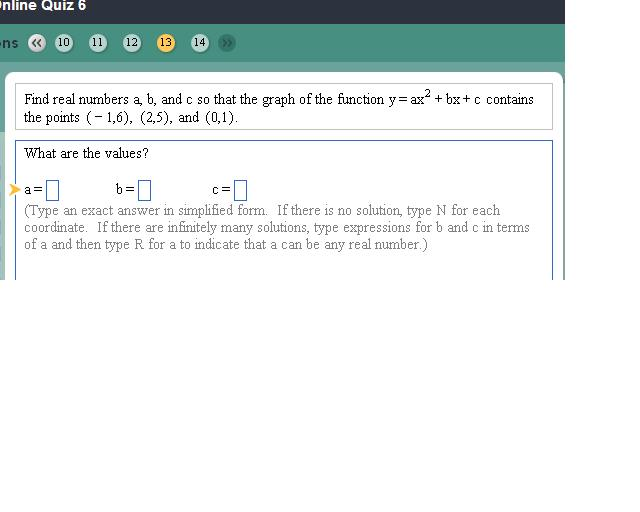



Find Real Numbers A B And C So That The Graph Of Chegg Com



Y Ax2 Bx C Quadratic Function Ppt Download
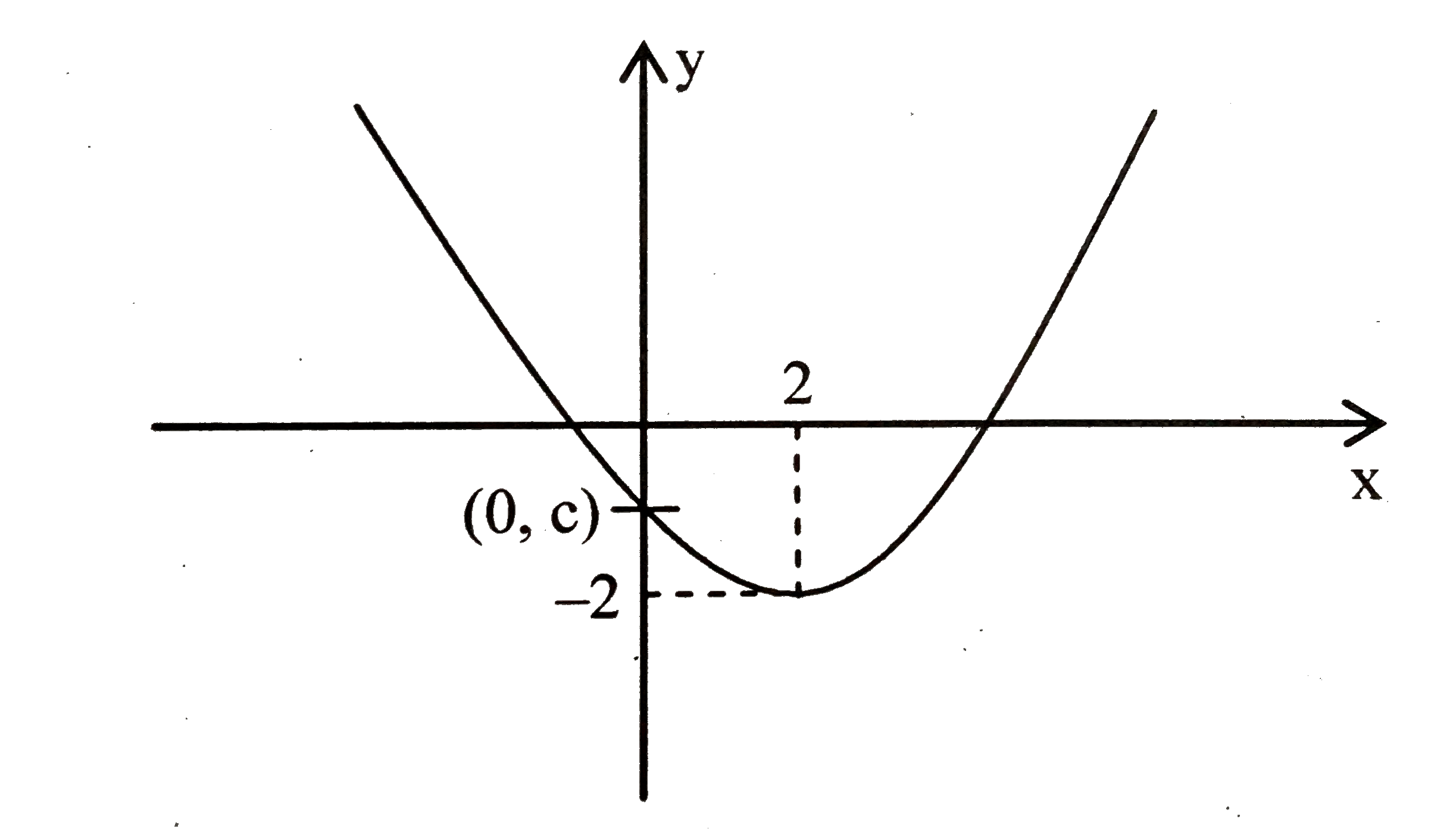
The graph of a quadratic function is a parabola The parabola can either be in "legs up" or "legs down" orientation We know that a quadratic equation will be in the form y = ax 2 bx c Our job is to find the values of a, b and c after first observing the graph




Y Ax2 Bx C Graph Novocom Top
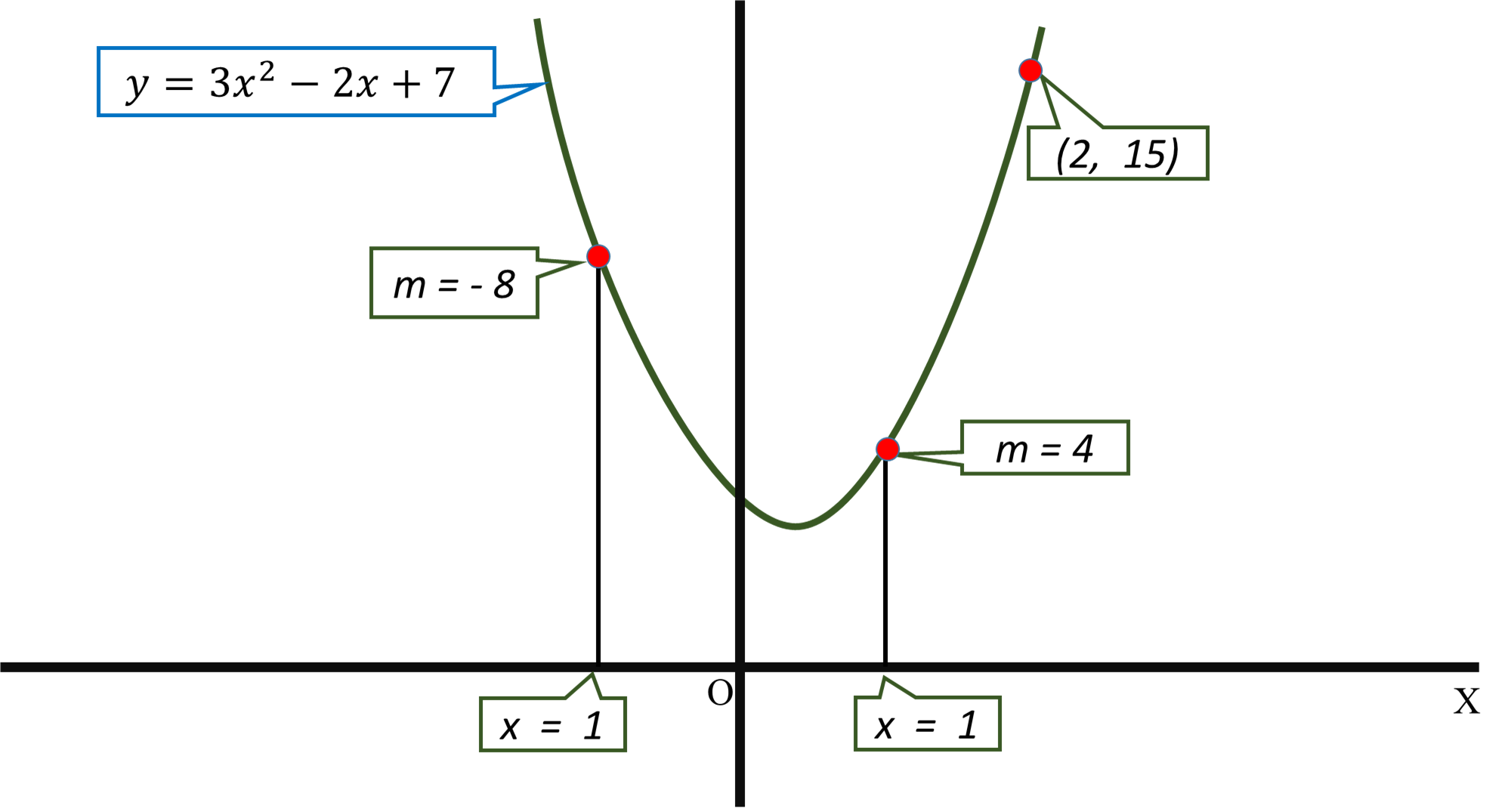



How Do You Find A Parabola With Equation Y Ax 2 Bx C That Has Slope 4 At X 1 Slope 8 At X 1 And Passes Through 2 15 Socratic
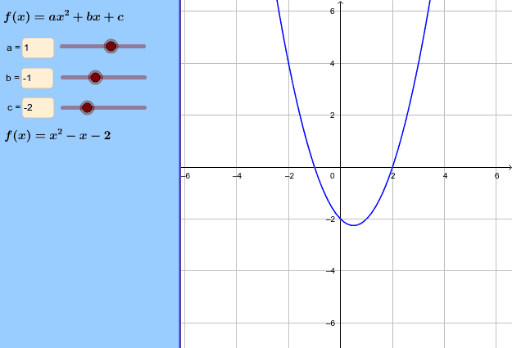



The Graph Of Y Ax 2 Bx C Geogebra



Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola




Graphing Y Ax 2 Bx C




Quadratic Function Wikipedia



The Graph Of The Polynomial Y Ax2 Bx C Is Shown In Fig 2 2 Write The Value Of B2 4ac Y Ax2 Bx C From Mathematics Polynomials Class 10 Haryana Board English Medium



If Y Ax 2 Bx C Represents A Parabola With Vertex A As Shown In The Figure And B 2 2 B 2ac Sarthaks Econnect Largest Online Education Community



Grafiek Kwadratisch




Effect Of A B C On Quadratic Youtube




The Adjoining Figure Shows The Graph Of Y Ax 2 Bx C Then Youtube



View Question What Do A B And C Mean In Y Ax 2 Bx C




Given That F X Ax 2 B X C And F X Y F X F Y Xy For Problem Solving Ps




Y Ax 2 Bx C What Is B




Which Of The Following Is An Equation In The Form Y Ax2 Bx C Of The Parabola Shown In The Brainly Com
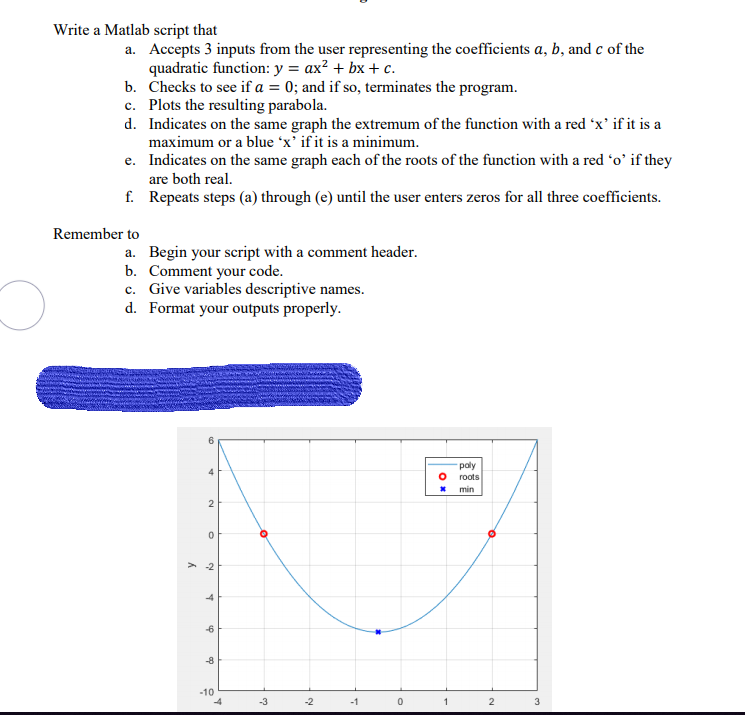



Write A Matlab Script That Accepts 3 Inputs From The Chegg Com
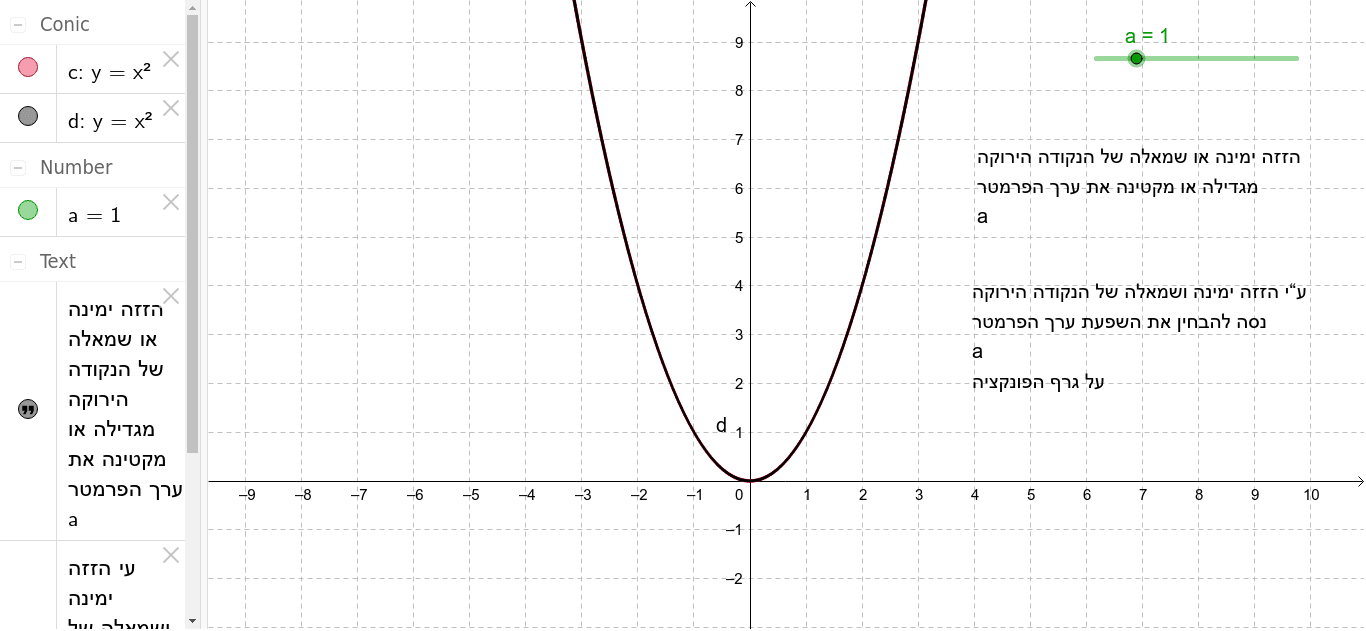



Y Ax 2 Bx C Geogebra




8 A Suppose That The Variable Y Is Known To Be A Chegg Com




B Value Definition Explanation Video Lesson Transcript Study Com



Exploring Parabolas Y Ax 2 Bx C
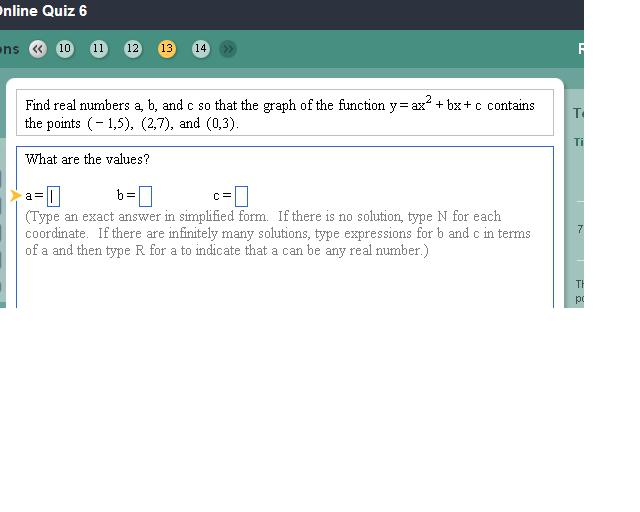



Find Real Numbers A B And C So That The Graph Of The Chegg Com
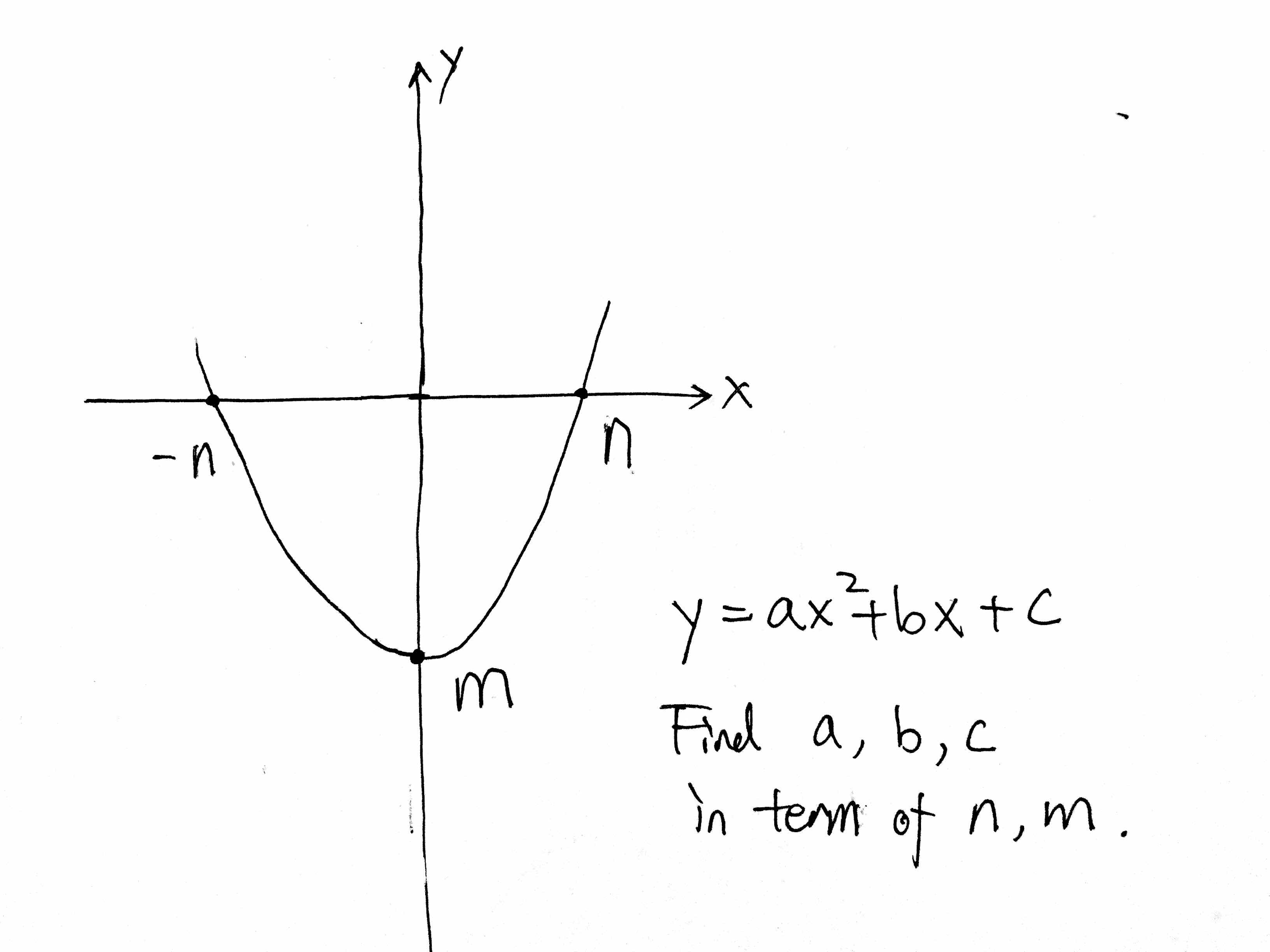



Y Ax 2 Bx C Find A B C In Term Of N M Chegg Com




Graphing Quadratics



The Graph Of Y Ax 2 Bx C Has A Minimum At 5 3 And Passes Through 4 0 How Do I Find The Values Of A B And C Quora




Suppose That A Parabola Y Ax 2 Bx C Where A 0 And A B C Is An Integer Has Vertex 1 4 9 8 If The Minimum Positive Value Of A




Quadratic Equation Handwiki




Equation Model Of Sorption Curve Y Ax 2 Bx C And Soil K Download Table
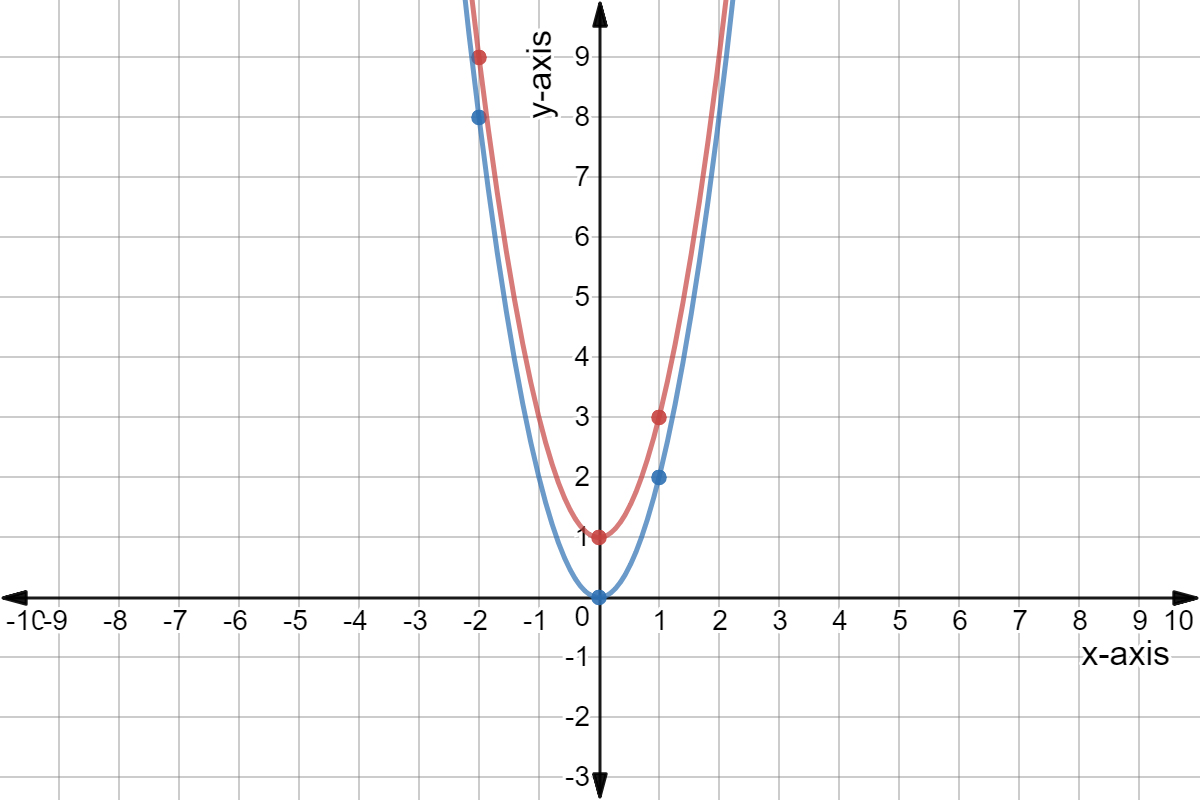



Quadratic Graph Example Y Ax C Expii



To Investigate The Effect Of The Constants A B And C On The Graph Y Ax2 Bx C Gcse Maths Marked By Teachers Com



The Curve Y Ax 2 Bx C Passes Through The Point Chegg Com




Quadratic Function Y Ax 2 Bx C Quadratic
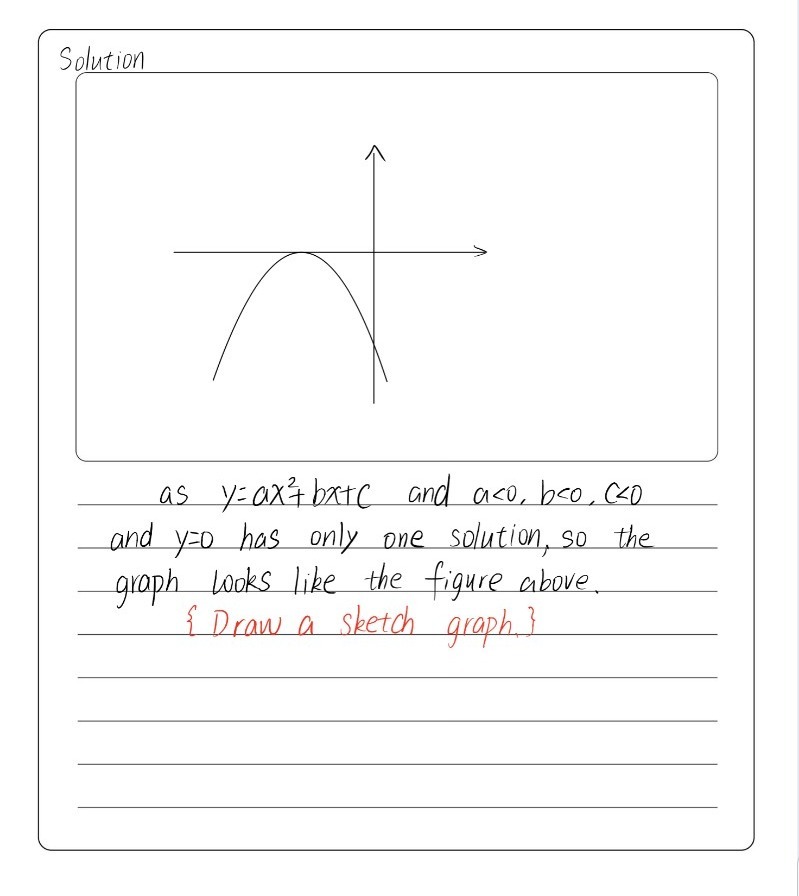



Draw A Sketch Graph Of Y Ax2 Bx C Where A 0 B 0 Gauthmath



Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola




The Expression Y Ax 2 Bx C Has Always The Same Sign As Of A If A 4ac Lt B 2 B 4ac Youtube




Straight Line Graphs Linear Graphs Ppt Download



Quadratic Graph Example Y Ax C Expii




Quadratic Formula Calculator



1



3




Graphing Quadratic Functions Ppt Download




If The Diagram In Fig 2 22 Shows The Graph Of The Polynomial F X Ax Bx C Then A A Gt 0 Brainly In
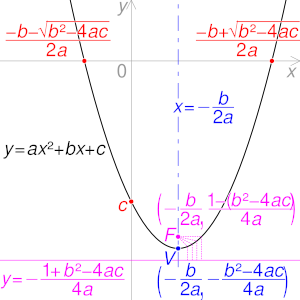



Quadratic Equation Handwiki



Q Tbn And9gcskitjvtu4g6u7oh5r8z42jlb391urt3idlmfdbjguuxli7v2fo Usqp Cau




0101 Graphing Quadratic Functions



To Investigate The Effect Of The Constants A B And C On The Graph Y Ax2 Bx C Gcse Maths Marked By Teachers Com




Consider The Following Formulae Y Ax2 Bx C Z 1 Gauthmath




The Roots Of A Quadratic Equation Y Ax2 Bx C Chegg Com



1




In The Equation Y Ax2 Bx C A B And C Are Cons Gauthmath




Clockwise Markers For The Functions Linear Y Ax B Quadratic Y Download Scientific Diagram



What Are The Coefficients A B And C Of The Parabola Y Ax 2 Bx C That Passes Through The Point 3 13 And Tangent To The Line 8x Y 15 At 2 1 Quora




A Parabola Y Ax2 Bx C Has A Y Intercept Of 5 And P Gauthmath
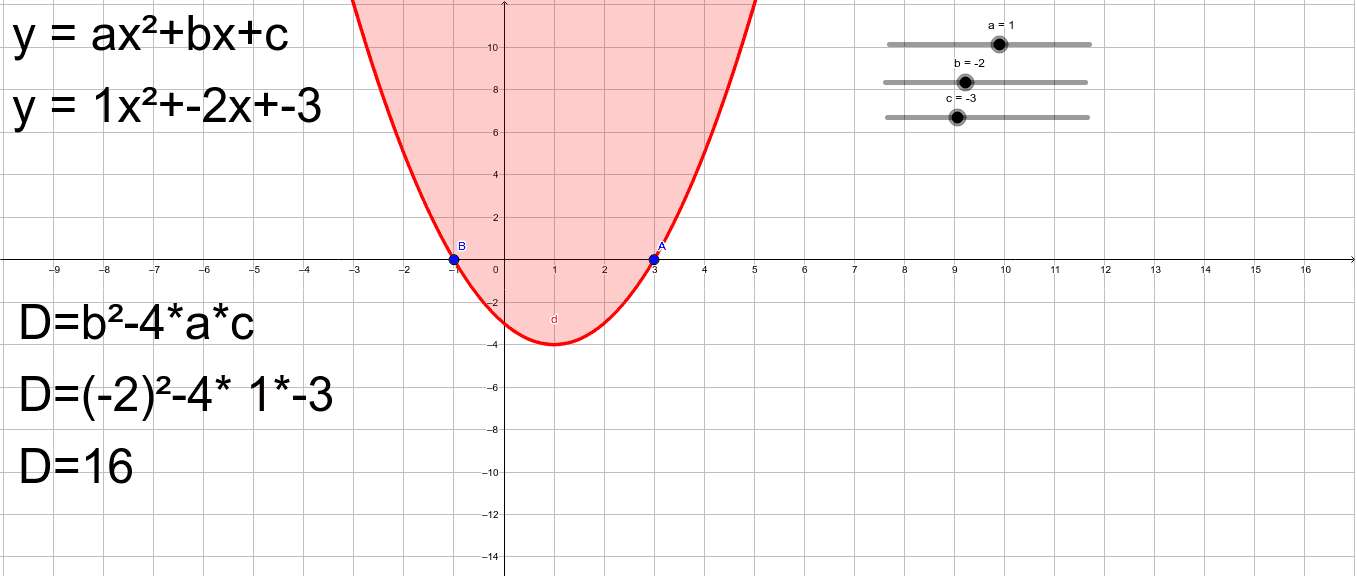



Y Ax 2 Bx C Geogebra




Graph Of Y Ax 2 Bx C Novocom Top




Find Constants A B And C Such That The Function Y Chegg Com
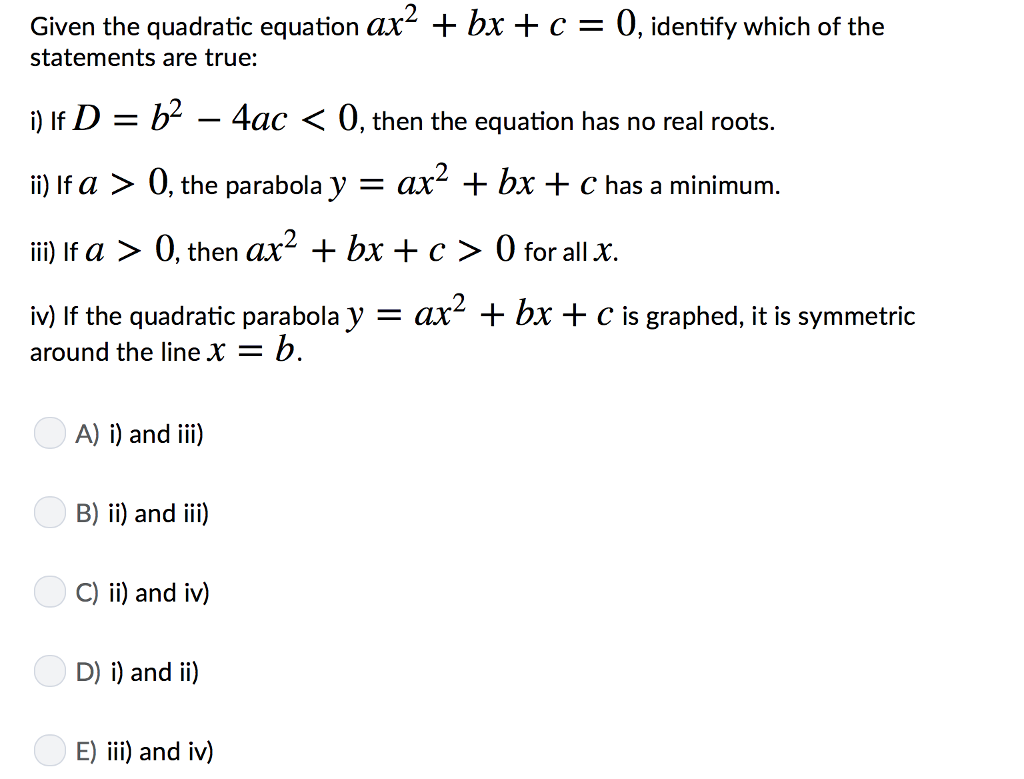



Given The Quadratic Equation Ax2 Bx C 0 Identify Chegg Com
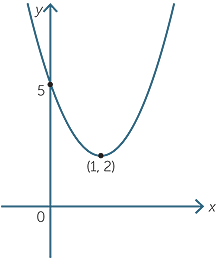



Quadratic Function




The Tangent To Y Ax 2 Bx C At 1 2 Is Parallel To The Normal At The Point 2 2 On The Youtube
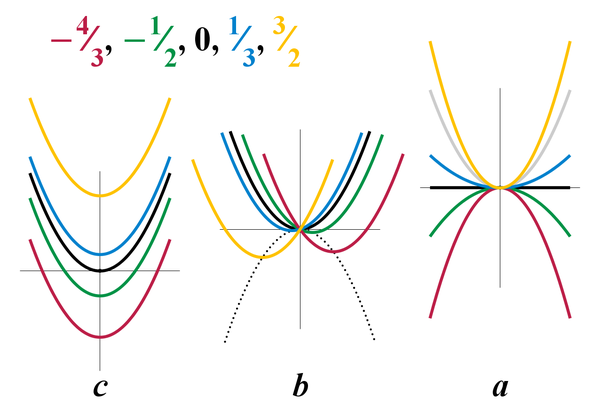



Quadratic Equation Wikiwand
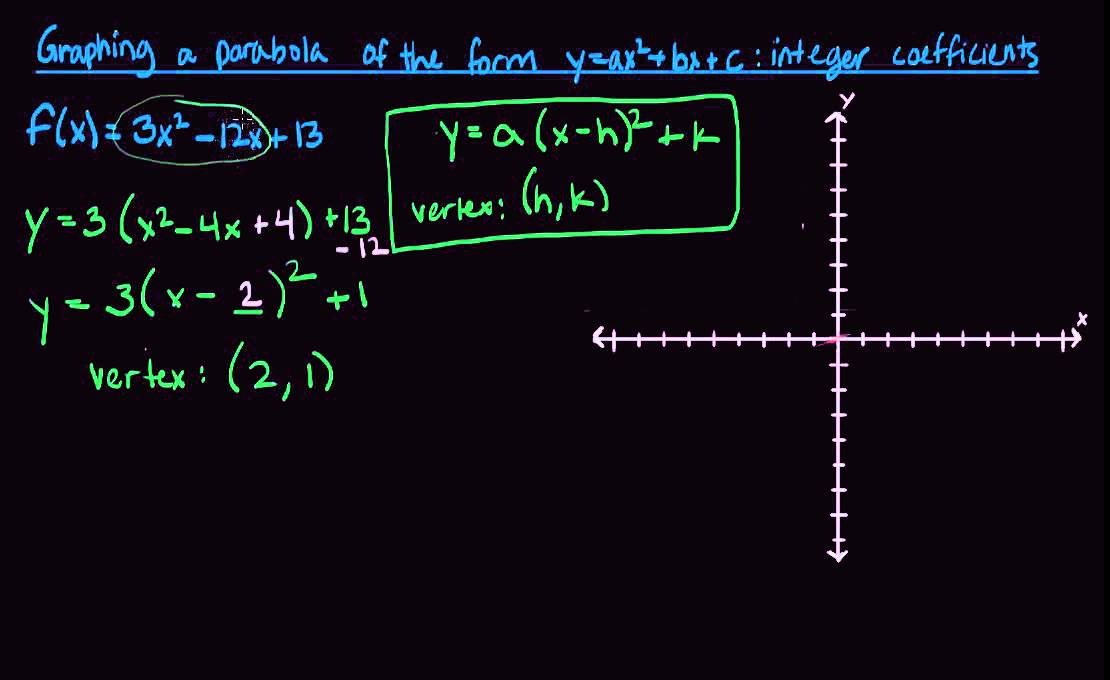



Graphing A Parabola Of The Form Y Ax2 Bx C With Integer Coefficients Youtube



How To Show That The Vertex Of The Parabola Math Y Ax 2 Bx C Math Can Be Expressed As Math B 2a C B 2 4a Math Quora



Form The Differential Equation Having For Its General Solution Y Ax 2 Bx Sarthaks Econnect Largest Online Education Community




Classzone Chapter 4
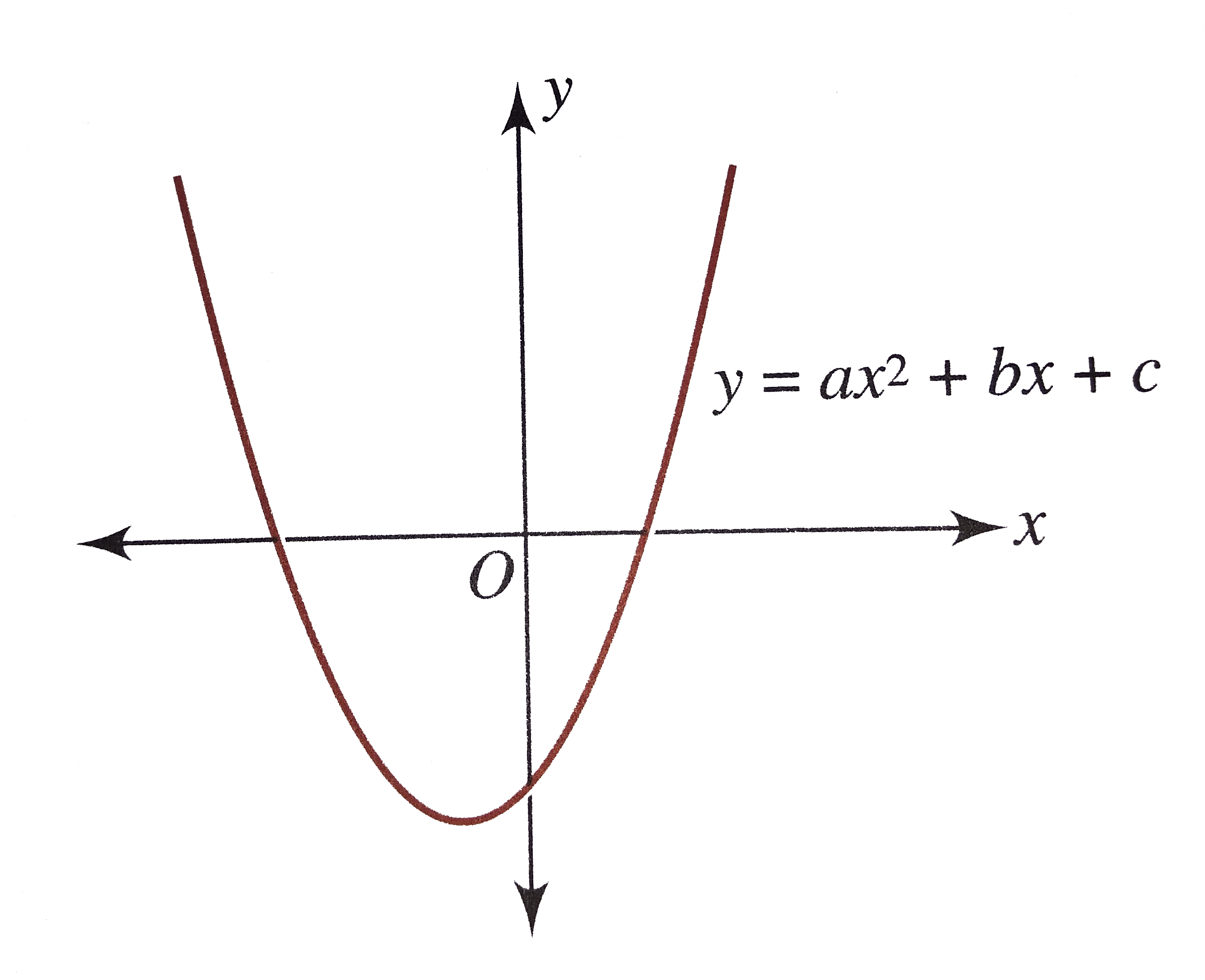



The Adjoining Figure Shows The Graph Of Y Ax 2 Bx C Then
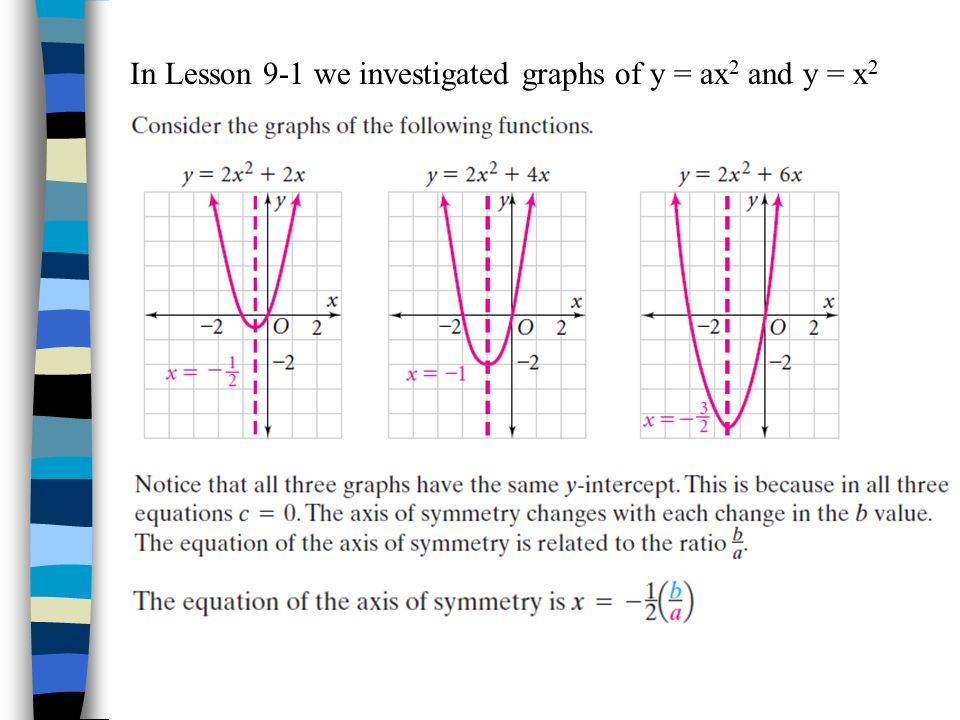



Lesson 9 2 Graphing Y Ax Bx C Objective To Graph Equations Of The Form F X Ax Bx C And Interpret These Graphs Ppt Download




54 The Graph Of Y Ax2 Bx C Is Shown In The Given Figu Scholr



If Y Ax 2 X A X B X C Bx X B X C C X C 1 Then Prove That 1 Y Dy Dx 1 X A A X
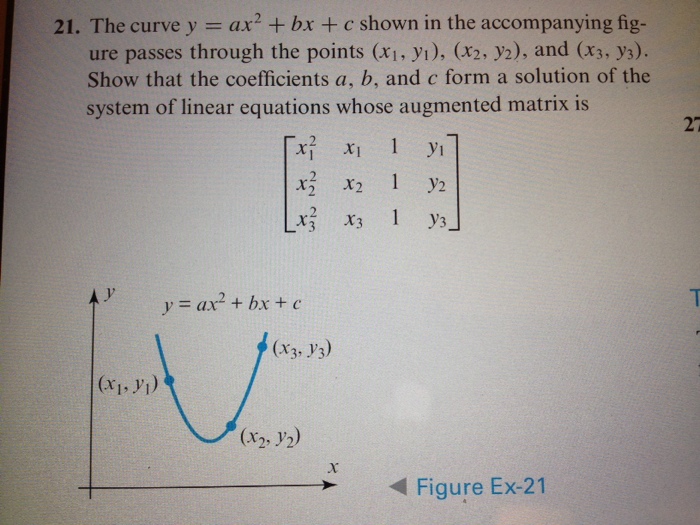



The Curve Y Ax2 Bx C Shown In The Accompanying Chegg Com




The Graphs Of The Two Equations Y A X 2 B X C And Y A X 2 B X C Such That Brainly In



Joerg Endrullis



Alg 1 Graphing Y Ax2 Bx C In A Powerpoint Presentation Tpt
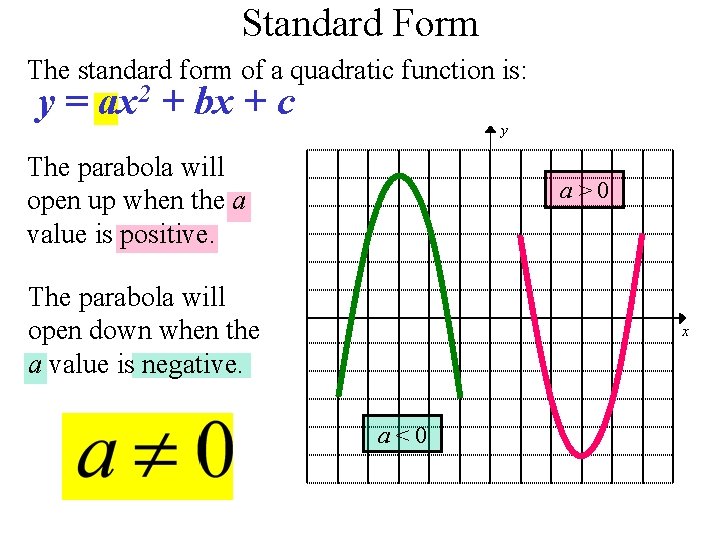



Quadratic Function Y Ax 2 Bx C Quadratic




Kwadratische Vergelijkingen Oplossen Y Ax2 Bx C Video 2 Wiskunde Tv Youtube
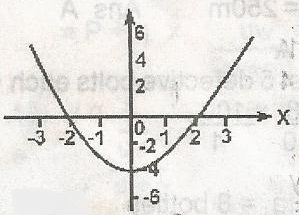



The Sketch Is The Curve Of Y Ax2 Bx C Find A Myschool


